完全二叉树是什么结构
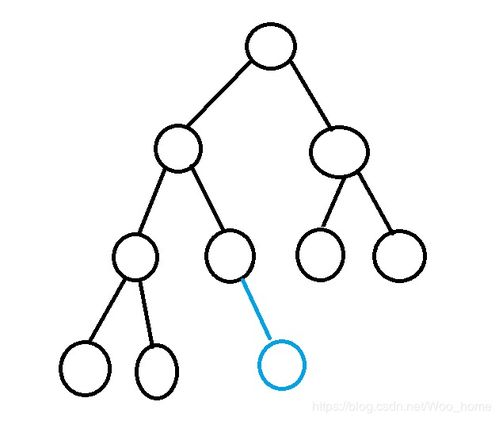
什么是完全二叉树?。
定义
。
完全二叉树是一种特殊的二叉树,其中除了最后一层之外,每一层的所有节点都有两个子节点。最后一层的节点可以具有零个或一个子节点,并且它们都必须在同一侧。
完全二叉树的特征。
形状
。
完全二叉树的形状与一个金字塔相似,每一层都有与前一层相同的节点数量。
高度
。
完全二叉树的高度是最小的高度,使其能够包含所有节点。高度计算公式为 ```log?(n) 1```,其中 n树中的节点数。
完全性
。
除了最后一层之外,完全二叉树中的每一层都完全填充。
应用。
查找表
。
完全二叉树常用于实现查找表,因为它们允许快速和有效的查找。
优先级队列
。
完全二叉树还可以实现优先级队列,其中具有最高优先级的元素存储在根节点中。
内存分配
。
完全二叉树在内存分配中也很有用,因为它们可以表示连续的内存块的分配。
完全二叉树是啥

完全二叉树是啥?

完全二叉树是一种特殊的二叉树结构,其中每一层上的节点数都达到最大可能值。换句话说,除了最后一层外,每一层的节点数都与完全二叉树可能的节点数相等。
完全二叉树的特点
完全二叉树具有以下特点:
除最后一层外,每一层都完全填满。
最后一层可能不完全填满,但所有节点都位于最左边。
每个节点有 0 个或 2 个子节点。
父节点位于子节点之间。
完全二叉树的优缺点
优点
空间利用率高。
查找、插入和删除操作效率较高。
易于实现和维护。
缺点
不平衡,可能导致搜索效率较低。
插入或删除操作可能导致树的结构发生变化,从而影响效率。
应用场景
完全二叉树常用于以下场景:
堆
优先队列
Huffma 编码
二叉搜索树
完全二叉树怎么构造

完全二叉树:构造方法详解
什么是完全二叉树?
完全二叉树是一种特殊的二叉树,其中所有层级都被完全填充,除了最后一层。最后一层可能不完全,但仍需尽地填充。
构造完全二叉树
方法 1:层序遍历
将元素逐层添加到树中,从根节点开始。对于每一层,从左到右添加元素。如果当前层已满,则继续下一层。
方法 2:递归
以根节点开始,创建左右子树。对于每个子树,递归地应用以下规则:
如果子树已满,则返回。
否则,为子树添加一个左子节点和一个右子节点。
方法 3:逐层构造
从根节点开始,逐层构造树。对于每一层:
计算该层中节点的数量。
逐个添加节点,从左到右。
对于最后一层,只添加足够数量的节点以填满该层。
实例
构造一个包含元素 [1, 2, 3, 4, 5, 6, 7] 的完全二叉树:
方法 1:层序遍历
```
1
/
2 3
/
4 5 6
/
7
```
方法 2:递归
```
1
/
2 3
/
4 5 6
/
7
```
方法 3:逐层构造
```
1
/
2 3
/
4 5 6
/
7
```
优点和缺点
优点:
高效搜索和插入操作。
易于实现和维护。
缺点:
可能浪费空间,因为最后一层可能不完全。
删除操作可能复杂,因为需要重新平衡树。
什么叫完全二叉树
什么叫完全二叉树?
定义
完全二叉树是一种特殊的二叉树结构,它除了最后一层外,每一层都完全填充着节点。最后一层的节点可能全部存在,也可能部分存在,但它们必须从左到右连续排列。
特征
完全二叉树具有以下特征:
高度平衡:完全二叉树的高度总是比具有相同节点数的任何其他二叉树要低。
节点数量:具有 层的完全二叉树具有 2^ - 1 个节点。
形状:完全二叉树具有金字塔形状,每一层比上一层包含更多的节点。
完全二叉树的优点
存储效率:完全二叉树可以以紧凑的方式存储数据,减少内存浪费。
搜索效率:因为完全二叉树是高度平衡的,所以搜索算法可以在 O(log ) 时间内找到节点。
插入和删除效率:在完全二叉树中插入和删除节点的操作相对简单,通常需要 O(log ) 时间。
完全二叉树的应用
完全二叉树在计算机科学中有着广泛的应用,包括:
堆:堆是一种基于完全二叉树实现的数据结构,用于实现优先级队列和其他操作。
哈夫曼树:哈夫曼树是一种基于完全二叉树实现的无损数据压缩算法。
本文采摘于网络,不代表本站立场,转载联系作者并注明出处:http://yihuasong.com/shu/7702.html
