什么是二叉树

什么是完全二叉树

什么是二叉树

什么是二叉树？

。

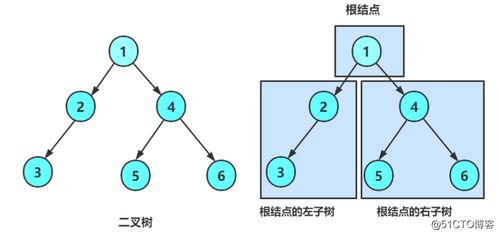
二叉树是一种数据结构，它由一组具有最多两个子节点（称为左孩子和右孩子）的节点组成。它是一个层次结构，其中每个节点都可以具有一个值，并且可以通过称为指针或引用的链接连接到子节点。

二叉树的组成部分。

节点

。

二叉树中的基本元素是节点，它包含以下属性：

。

值：存储在节点中的数据。。

左孩子：指向左子节点的指针或引用。如果不存在左子节点，则为 null。。

右孩子：指向右子节点的指针或引用。如果不存在右子节点，则为 null。。

。

根节点

。

二叉树的根节点是树的起点，它没有父节点。

叶子节点

。

二叉树中的叶子节点是没有任何子节点的节点。

高度

。

二叉树的高度是树中从根节点到最深叶子节点的节点数。

树的类型

。

二叉树有两种主要类型：。

完整二叉树：所有非叶子节点都有两个子节点。

完全二叉树：所有叶子节点都在同一层上。

什么是完全二叉树

什么是完全二叉树？

定义

完全二叉树是指一棵二叉树，其中除了最后一层外，每一层都完全填满。最后一层可能只有少于完全容量的节点，但是这些节点必须从左到右连续排列。

特点

完全二叉树具有以下特点：

节点数奇偶性与层数有关：如果一棵完全二叉树有 层，那么它具有 2 - 1 个节点。

最后一个节点在最右边的层上。

每个节点都有两个子节点或没有子节点。

优点

完全二叉树具有以下优点：

空间利用效率高，可以最大限度地利用内存空间。

搜索和插入操作的效率很高，因为树是平衡的。

可以轻松地转换为堆数据结构，用于优先队列等应用。

算法

有几种算法可以用来创建或遍历完全二叉树：

层序遍历

广度优先搜索

高度平衡树

应用

完全二叉树在各种计算机科学应用中都有使用，包括：

堆

优先队列

哈夫曼编码

动态规划