具体来说，对于一个具有左右子树的节点，后序遍历的顺序是：左子树 -> 右子树 -> 节点。对于没有子树的节点，只需要访问节点本身。

    在Python中，后序遍历的实现通常使用递归方式，代码如下：

    ```python

    class TreeNode:

     def __init__(self, x):

     self.val = x

     self.left = None

     self.right = None

    def postorderTraversal(root):

     res = []

     if root:

     res = postorderTraversal(root.left)

     res = res + postorderTraversal(root.right)

     res.append(root.val)

     return res

    ```

    以上代码定义了一个二叉树节点的类（TreeNode），然后定义了一个后序遍历的函数（postorderTraversal）。这个函数首先检查根节点是否存在，如果存在，则先对左子树进行后序遍历，然后对右子树进行后序遍历，最后将根节点的值添加到结果列表中。

二叉树后序遍历：深入了解二叉树结构与遍历方法

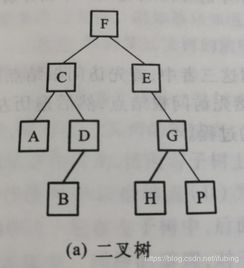
    二叉树是计算机科学中常见的数据结构，用于高效地存储和操作数据。在二叉树中，每个节点最多有两个子节点，通常称为左子节点和右子节点。为了更好地理解和操作二叉树，我们需要对其进行遍历。今天，我们将深入探讨二叉树的后序遍历。

一、什么是后序遍历？

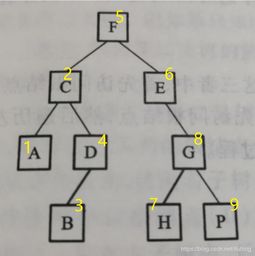
    后序遍历是二叉树遍历方法中的一种，其顺序为左子树、右子树、根节点。在后序遍历中，我们首先访问节点的左子树，然后访问节点的右子树，最后访问根节点。这种遍历方式对于二叉树的某些操作非常有用，如构建表达式树或执行某些计算。

二、后序遍历的递归实现

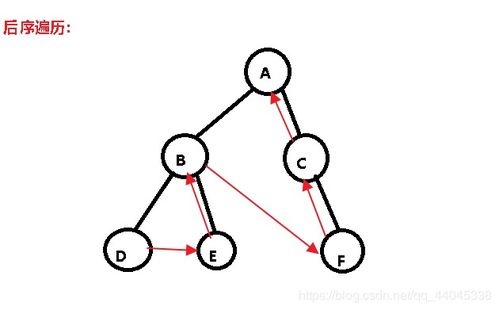
    在二叉树的后序遍历中，我们可以使用递归来实现。我们定义一个函数来遍历整个二叉树。在这个函数中，我们需要判断当前节点是否为空。如果当前节点为空，我们返回；否则，我们首先递归遍历左子树，然后递归遍历右子树，最后访问当前节点。

    在Pyho中，后序遍历的递归实现可以如下：

    ```pyho

    class Treeode:

     def __ii__(self, val=0, lef=oe, righ=oe):

     self.val = val

     self.lef = lef

     self.righ = righ

    def posorderTraversal(roo):

     if roo is oe:

     reur []

     reur posorderTraversal(roo.lef) + posorderTraversal(roo.righ) + [roo.val]

    ```

    在这个实现中，我们首先检查当前节点是否为空。如果为空，我们返回一个空列表。否则，我们递归遍历左子树和右子树，并将它们的结果与当前节点的值连接起来。这样，我们就得到了以当前节点为结尾的后序遍历结果。

三、后序遍历的非递归实现

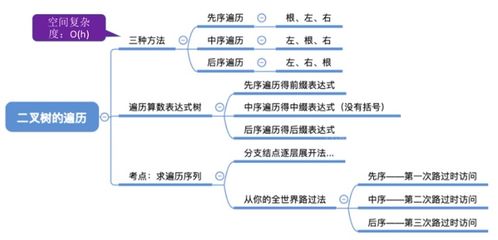
    虽然递归是实现后序遍历的常用方法，但有时我们可能需要使用非递归方法。非递归方法通常使用栈来模拟递归过程。下面是一个使用Pyho实现的后序遍历的非递归方法：

    ```pyho

    def posorderTraversal(roo):

     if roo is oe:

     reur []

     resul = []

     sack = [(roo, False)] # (ode, is_visied)

     while sack:

     ode, is_visied = sack.pop()

     if ode is oe: # Skip oe ode i he middle of he pah.

     coiue

     if is_visied: # If he ode is visied, apped i o he resul.

     resul.apped(ode.val)

     else: # If he ode is o visied, mark i as visied ad push is childre io he sack.

     sack.apped((ode, True))

     sack.apped((ode.lef, False))

     sack.apped((ode.righ, False))

     reur resul[::-1] # Reverse he resul lis o ge he posorder raversal.

    ```

    在这个实现中，我们使用一个栈来存储节点和它们的访问状态。我们首先将根节点和它的访问状态（未访问）压入栈中。然后，我们不断地从栈中弹出一个节点和它的访问状态。如果节点的访问状态为False（未访问），则将它和True（已访问）压入栈中，并将它的左子节点和右子节点压入栈中。如果节点的访问状态为True（已访问），则将它添加到结果列表中。我们将结果列表反转以得到后序遍历的结果。